LogLogisticFitter¶

class lifelines.fitters.log_logistic_fitter.LogLogisticFitter(*args, **kwargs)¶

This class implements a Log-Logistic model for univariate data. The model has parameterized form:

\[S(t) = \left(1 + \left(\frac{t}{\alpha}\right)^{\beta}\right)^{-1}, \alpha > 0, \beta > 0,\]

The \(\alpha\) (scale) parameter has an interpretation as being equal to the median lifetime of the population. The \(\beta\) parameter influences the shape of the hazard. See figure below:

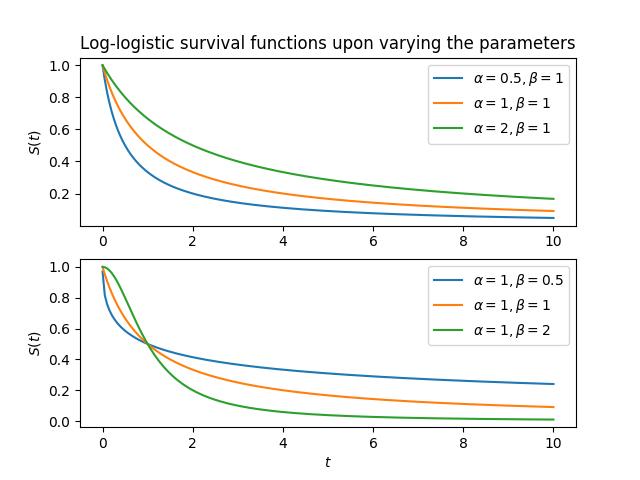
The hazard rate is:

\[h(t) = \frac{\left(\frac{\beta}{\alpha}\right)\left(\frac{t}{\alpha}\right) ^ {\beta-1}}{\left(1 + \left(\frac{t}{\alpha}\right)^{\beta}\right)}\]

and the cumulative hazard is:

\[H(t) = \log\left(\left(\frac{t}{\alpha}\right) ^ {\beta} + 1\right)\]

After calling the .fit method, you have access to properties like: cumulative_hazard_, plot, survival_function_, alpha_ and beta_. A summary of the fit is available with the method ‘print_summary()’

Parameters:: alpha (float, optional (default=0.05)) – the level in the confidence intervals.

Examples

from lifelines import LogLogisticFitter
from lifelines.datasets import load_waltons
waltons = load_waltons()

llf = LogLogisticFitter()
llf.fit(waltons['T'], waltons['E'])
llf.plot()
print(llf.alpha_)

cumulative_hazard_¶

The estimated cumulative hazard (with custom timeline if provided)

Type:: DataFrame

hazard_¶

The estimated hazard (with custom timeline if provided)

Type:: DataFrame

survival_function_¶

The estimated survival function (with custom timeline if provided)

Type:: DataFrame

cumulative_density_¶

The estimated cumulative density function (with custom timeline if provided)

Type:: DataFrame

density_¶

The estimated density function (PDF) (with custom timeline if provided)

Type:: DataFrame

variance_matrix_¶

The variance matrix of the coefficients

Type:: DataFrame

median_survival_time_¶

The median time to event

Type:: float

alpha_¶

The fitted parameter in the model

Type:: float

beta_¶

The fitted parameter in the model

Type:: float

durations¶

The durations provided

Type:: array

event_observed¶

The event_observed variable provided

Type:: array

timeline¶

The time line to use for plotting and indexing

Type:: array

entry¶

The entry array provided, or None

Type:: array or None

alpha_: float¶

beta_: float¶

property median_survival_time_¶: Return the unique time point, t, such that S(t) = 0.5. This is the “half-life” of the population, and a robust summary statistic for the population, if it exists.

percentile(p)¶

Return the unique time point, t, such that S(t) = p.

Parameters:: p (float)