More examples and recipes¶
This section goes through some examples and recipes to help you use lifelines.
Worked Examples¶
If you are looking for some full examples of lifelines, there are full Jupyter notebooks and scripts here and examples and ideas on the development blog.
Statistically compare two populations¶
Often researchers want to compare survival-ness between different populations. Here are some techniques to do that:
Logrank test¶
Note
The logrank test has maximum power when the assumption of proportional hazards is true. As a consequence, if the survival functions cross, the logrank test will give an inaccurate assessment of differences.
The lifelines.statistics.logrank_test() function compares whether the “death” generation process of the two populations are equal:
from lifelines.statistics import logrank_test
from lifelines.datasets import load_waltons
df = load_waltons()
ix = df['group'] == 'miR-137'
T_exp, E_exp = df.loc[ix, 'T'], df.loc[ix, 'E']
T_con, E_con = df.loc[~ix, 'T'], df.loc[~ix, 'E']
results = logrank_test(T_exp, T_con, event_observed_A=E_exp, event_observed_B=E_con)
results.print_summary()
"""
t_0 = -1
alpha = 0.95
null_distribution = chi squared
df = 1
use_bonferroni = True
---
test_statistic p
3.528 0.00034 **
"""
print(results.p_value) # 0.46759
print(results.test_statistic) # 0.528
If you have more than two populations, you can use pairwise_logrank_test() (which compares
each pair in the same manner as above), or multivariate_logrank_test() (which tests the
hypothesis that all the populations have the same “death” generation process).
import pandas as pd
from lifelines.statistics import multivariate_logrank_test
df = pd.DataFrame({
'durations': [5, 3, 9, 8, 7, 4, 4, 3, 2, 5, 6, 7],
'groups': [0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2], # could be strings too
'events': [1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0],
})
results = multivariate_logrank_test(df['durations'], df['groups'], df['events'])
results.print_summary()
"""
t_0 = -1
alpha = 0.95
null_distribution = chi squared
df = 2
---
test_statistic p
1.0800 0.5827
---
"""
The logrank test statistic is calculated from the differences between the observed deaths for a group and expected deaths, under the null hypothesis that all groups share the same survival curve, summed across all ordered death times. It therefore weights differences between the survival curves equally at each death time, resulting in maximum power when the assumption of proportional hazards is true. To test for early or late differences in survival between groups, a weighted logrank test that are more sensitive to non-proportional hazards might be a better choice.
Four types of weighted logrank test are currently available in lifelines through the weightings argument:
the Wilcoxon (weightings='wilcoxon'), Tarone-Ware (weightings='tarone-ware'), Peto (weightings='peto')
and Fleming-Harrington (weightings='fleming-harrington') tests.
The following weightings are applied at the ith ordered failure time, \(t_{i}\):
\[\text{Wilcoxon:}\quad n_i\]\[\text{Tarone-Ware:}\quad \sqrt{n_i}\]\[\text{Peto:}\quad \bar{S}(t_i)\]\[\text{Fleming-Harrington}\quad \hat{S}(t_i)^p \times (1 - \hat{S}(t_i))^q\]
where \(n_i\) is the number at risk just prior to time \(t_{i}\), \(\bar{S}(t_i)\) is Peto-Peto’s modified survival estimate and \(\hat{S}(t_i)\) is the left-continuous Kaplan-Meier survival estimate at time \(t_{i}\).
The Wilcoxon, Tarone-Ware and Peto tests apply more weight to earlier death times. The Peto test is more robust than the Wilcoxon or Tarone-Ware tests when many observations are censored. When p > q, the Fleming-Harrington applies more weight to earlier death times whilst when p < q, it is more sensitive to late differences (for p=q=0 it reduces to the unweighted logrank test). The choice of which test to perform should be made in advance and not retrospectively to avoid introducing bias.
import pandas as pd
from lifelines.statistics import multivariate_logrank_test
df = pd.DataFrame({
'durations': [5, 3, 9, 8, 7, 4, 4, 3, 2, 5, 6, 7],
'groups': [0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2], # could be strings too
'events': [1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0],
})
results = multivariate_logrank_test(df['durations'], df['groups'], df['events'], weightings='peto')
results.print_summary()
"""
t_0 = -1
null_distribution = chi squared
degrees_of_freedom = 2
test_name = multivariate_Peto_test
---
test_statistic p -log2(p)
0.95 0.62 0.68
"""
Survival differences at a point in time¶
Often analysts want to compare the survival-ness of groups at specific times, rather than comparing the entire survival curves against each other. For example, analysts may be interested in 5-year survival. Statistically comparing the naive Kaplan-Meier points at a specific time
actually has reduced power. By transforming the Kaplan-Meier curve, we can recover more power. The function lifelines.statistics.survival_difference_at_fixed_point_in_time_test() uses
the log(-log) transformation implicitly and compares the survival-ness of populations at a specific point in time using chi-squared test.
from lifelines.statistics import survival_difference_at_fixed_point_in_time_test
from lifelines.datasets import load_waltons
df = load_waltons()
ix = df['group'] == 'miR-137'
T_exp, E_exp = df.loc[ix, 'T'], df.loc[ix, 'E']
T_con, E_con = df.loc[~ix, 'T'], df.loc[~ix, 'E']
kmf_exp = KaplanMeierFitter(label="exp").fit(T_exp, E_exp)
kmf_con = KaplanMeierFitter(label="con").fit(T_con, E_con)
point_in_time = 10.
results = survival_difference_at_fixed_point_in_time_test(point_in_time, kmf_exp, kmf_con)
results.print_summary()
"""
t_0 = -1
null_distribution = chi squared
degrees_of_freedom = 1
point_in_time = 10.0
test_name = survival_difference_at_fixed_point_in_time_test
---
test_statistic p -log2(p)
4.77 0.03 5.11
"""
Moreover, we can plot the two survival curves and compare them at the fixed point in time:
kmf_exp.plot_survival_function(point_in_time=point_in_time)
kmf_con.plot_survival_function(point_in_time=point_in_time)

We can see that the expermintal’s survival function value (blue) is lower than the control’s group value (orange). It is worth observing that at that particular point, the confidence intervals for both groups overlap to some extent, which is not consistently observed at all other time points.
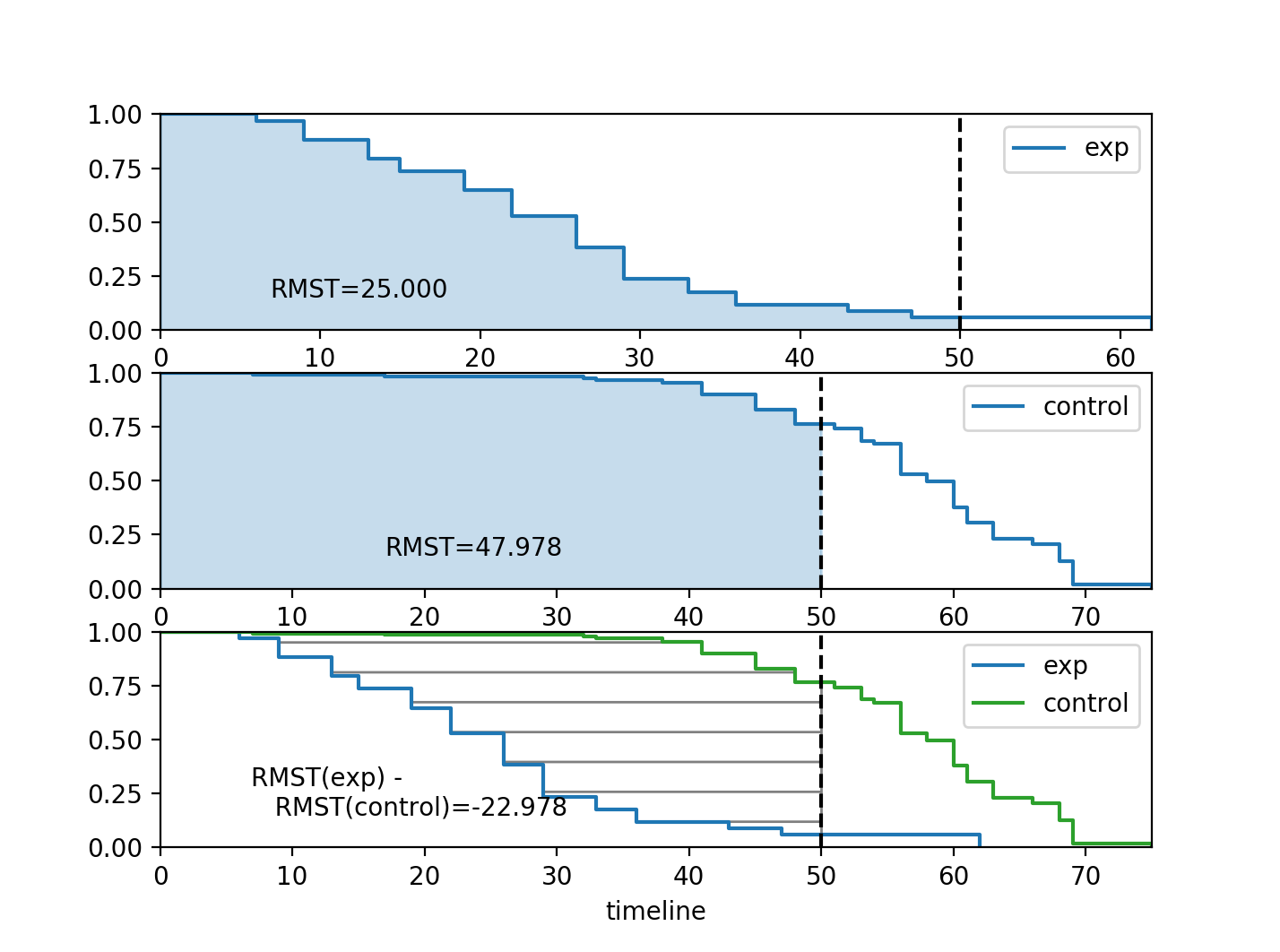
Restricted mean survival times (RMST)¶
lifelines has a function to accurately compute the restricted mean survival time, defined as
\[\text{RMST}(t) = \int_0^t S(\tau) d\tau\]
This is a good metric for comparing two survival curves, as their difference represents the area between the curves (see figure below) which is a measure of “time lost”. The upper limit of the integral above is often finite because the tail of the estimated survival curve has high variance and can strongly influence the integral.
from lifelines.utils import restricted_mean_survival_time
from lifelines.datasets import load_waltons
from lifelines import KaplanMeierFitter
df = load_waltons()
ix = df['group'] == 'miR-137'
T, E = df['T'], df['E']
time_limit = 50
kmf_exp = KaplanMeierFitter().fit(T[ix], E[ix], label='exp')
rmst_exp = restricted_mean_survival_time(kmf_exp, t=time_limit)
kmf_con = KaplanMeierFitter().fit(T[~ix], E[~ix], label='control')
rmst_con = restricted_mean_survival_time(kmf_con, t=time_limit)
Furthermore, there exist plotting functions to plot the RMST:
from matplotlib import pyplot as plt
from lifelines.plotting import rmst_plot
ax = plt.subplot(311)
rmst_plot(kmf_exp, t=time_limit, ax=ax)
ax = plt.subplot(312)
rmst_plot(kmf_con, t=time_limit, ax=ax)
ax = plt.subplot(313)
rmst_plot(kmf_exp, model2=kmf_con, t=time_limit, ax=ax)
Model selection using lifelines¶
If using lifelines for prediction work, it’s ideal that you perform some type of cross-validation scheme. This cross-validation allows you to be confident that your out-of-sample predictions will work well in practice. It also allows you to choose between multiple models.
lifelines has a built-in k-fold cross-validation function. For example, consider the following example:
import numpy as np
from lifelines import AalenAdditiveFitter, CoxPHFitter
from lifelines.datasets import load_regression_dataset
from lifelines.utils import k_fold_cross_validation
df = load_regression_dataset()
#create the three models we'd like to compare.
aaf_1 = AalenAdditiveFitter(coef_penalizer=0.5)
aaf_2 = AalenAdditiveFitter(coef_penalizer=10)
cph = CoxPHFitter()
print(np.mean(k_fold_cross_validation(cph, df, duration_col='T', event_col='E', scoring_method="concordance_index")))
print(np.mean(k_fold_cross_validation(aaf_1, df, duration_col='T', event_col='E', scoring_method="concordance_index")))
print(np.mean(k_fold_cross_validation(aaf_2, df, duration_col='T', event_col='E', scoring_method="concordance_index")))
From these results, Aalen’s Additive model with a penalizer of 10 is best model of predicting future survival times.
lifelines also has wrappers to use scikit-learn’s cross validation and grid search tools. See how to use lifelines with scikit learn.
Selecting a parametric model using QQ plots¶
QQ plots normally are constructed by sorting the values. However, this isn’t appropriate when there is censored data. In lifelines, there are routines to still create QQ plots with censored data. These are available under lifelines.plotting.qq_plots(), and accepts fitted a parametric lifelines model.
from lifelines import *
from lifelines.plotting import qq_plot
# generate some fake log-normal data
N = 1000
T_actual = np.exp(np.random.randn(N))
C = np.exp(np.random.randn(N))
E = T_actual < C
T = np.minimum(T_actual, C)
fig, axes = plt.subplots(2, 2, figsize=(8, 6))
axes = axes.reshape(4,)
for i, model in enumerate([WeibullFitter(), LogNormalFitter(), LogLogisticFitter(), ExponentialFitter()]):
model.fit(T, E)
qq_plot(model, ax=axes[i])
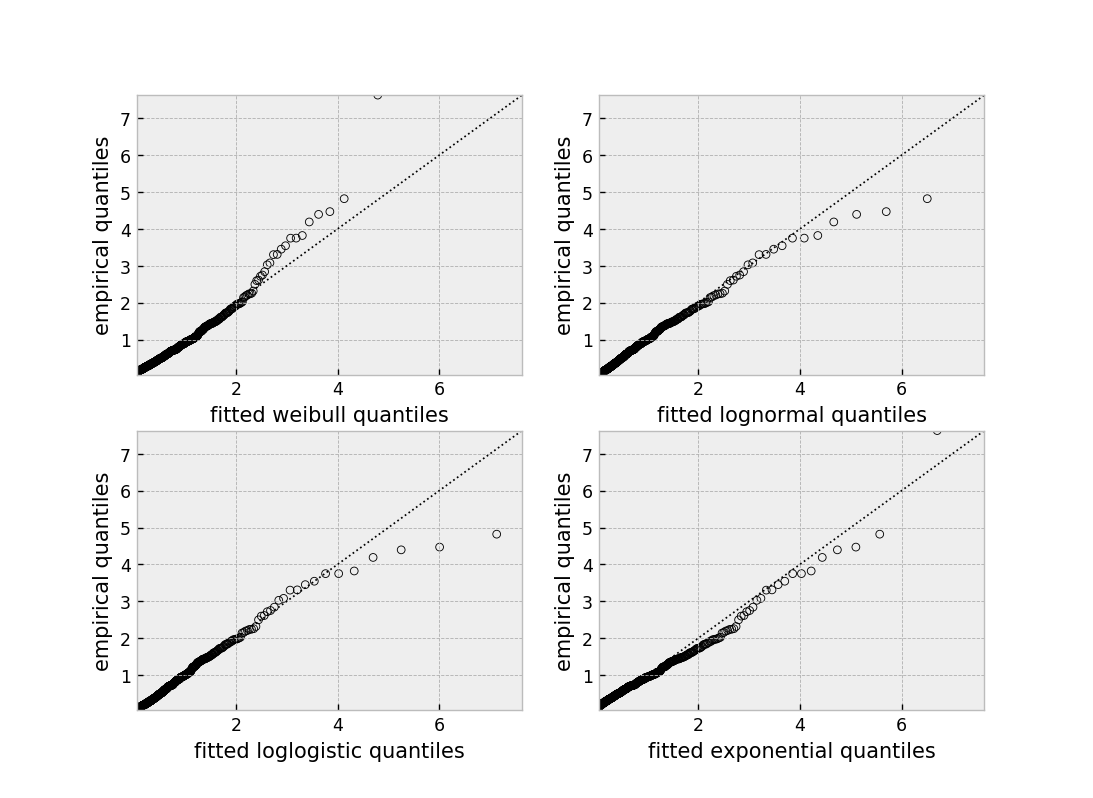
This graphical test can be used to invalidate models. For example, in the above figure, we can see that only the log-normal parametric model is appropriate (we expect deviance in the tails, but not too much). Another use case is choosing the correct parametric AFT model.
The qq_plots() also works with left censorship as well.
Selecting a parametric model using AIC¶
A natural way to compare different models is the AIC:
where \(k\) is the number of parameters (degrees-of-freedom) of the model and \(\text{ll}\) is the maximum log-likelihood. The model with the lowest AIC is desirable, since it’s a trade off between maximizing the log-likelihood with as few parameters as possible.
All lifelines models have the AIC_ property after fitting.
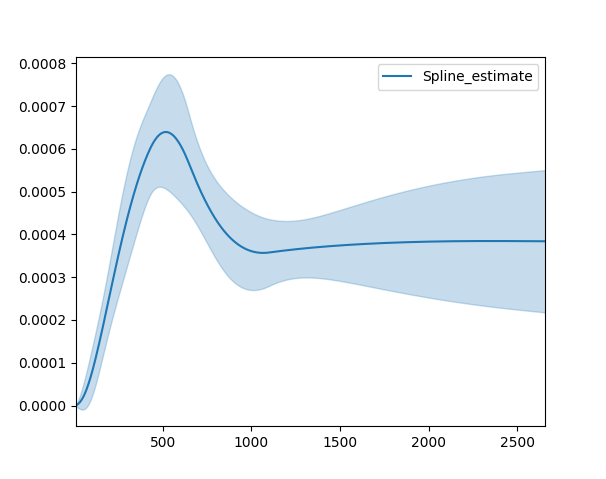
Further more, lifelines has a built in function to automate AIC comparisons between univariate parametric models:
from lifelines.utils import find_best_parametric_model
from lifelines.datasets import load_lymph_node
T = load_lymph_node()['rectime']
E = load_lymph_node()['censrec']
best_model, best_aic_ = find_best_parametric_model(T, E, scoring_method="AIC")
print(best_model)
# <lifelines.SplineFitter:"Spline_estimate", fitted with 686 total observations, 387 right-censored observations>
best_model.plot_hazard()
Plotting multiple figures on a plot¶
When .plot is called, an axis object is returned which can be passed into future calls of .plot:
kmf.fit(data1)
ax = kmf.plot_survival_function()
kmf.fit(data2)
ax = kmf.plot_survival_function(ax=ax)
If you have a pandas DataFrame with columns “T”, “E”, and some categorical variable, then something like the following would work:
from matplotlib import pyplot as plt
from lifelines.datasets import load_waltons
from lifelines import KaplanMeierFitter
df = load_waltons()
ax = plt.subplot(111)
kmf = KaplanMeierFitter()
for name, grouped_df in df.groupby('group'):
kmf.fit(grouped_df["T"], grouped_df["E"], label=name)
kmf.plot_survival_function(ax=ax)
Plotting interval censored data¶
Note
New in lifelines v0.24.6
from lifelines.datasets import load_diabetes
from lifelines.plotting import plot_interval_censored_lifetimes
df_sample = load_diabetes().sample(frac=0.02)
ax = plot_interval_censored_lifetimes(df_sample['left'], df_sample['right'])
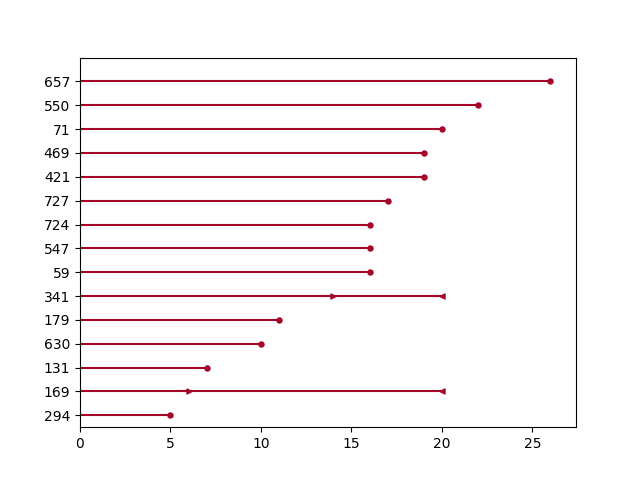
Plotting options and styles¶
Let’s load some data
from lifelines.datasets import load_waltons
waltons = load_waltons()
T = waltons['T']
E = waltons['E']
Standard¶
kmf = KaplanMeierFitter()
kmf.fit(T, E, label="kmf.plot_survival_function()")
kmf.plot_survival_function()

Show censors and edit markers¶
kmf.fit(T, E, label="kmf.plot_survival_function(show_censors=True, \ncensor_styles={'ms': 6, 'marker': 's'})")
kmf.plot_survival_function(show_censors=True, censor_styles={'ms': 6, 'marker': 's'})

Hide confidence intervals¶
kmf.fit(T, E, label="kmf.plot_survival_function(ci_show=False)")
kmf.plot_survival_function(ci_show=False)
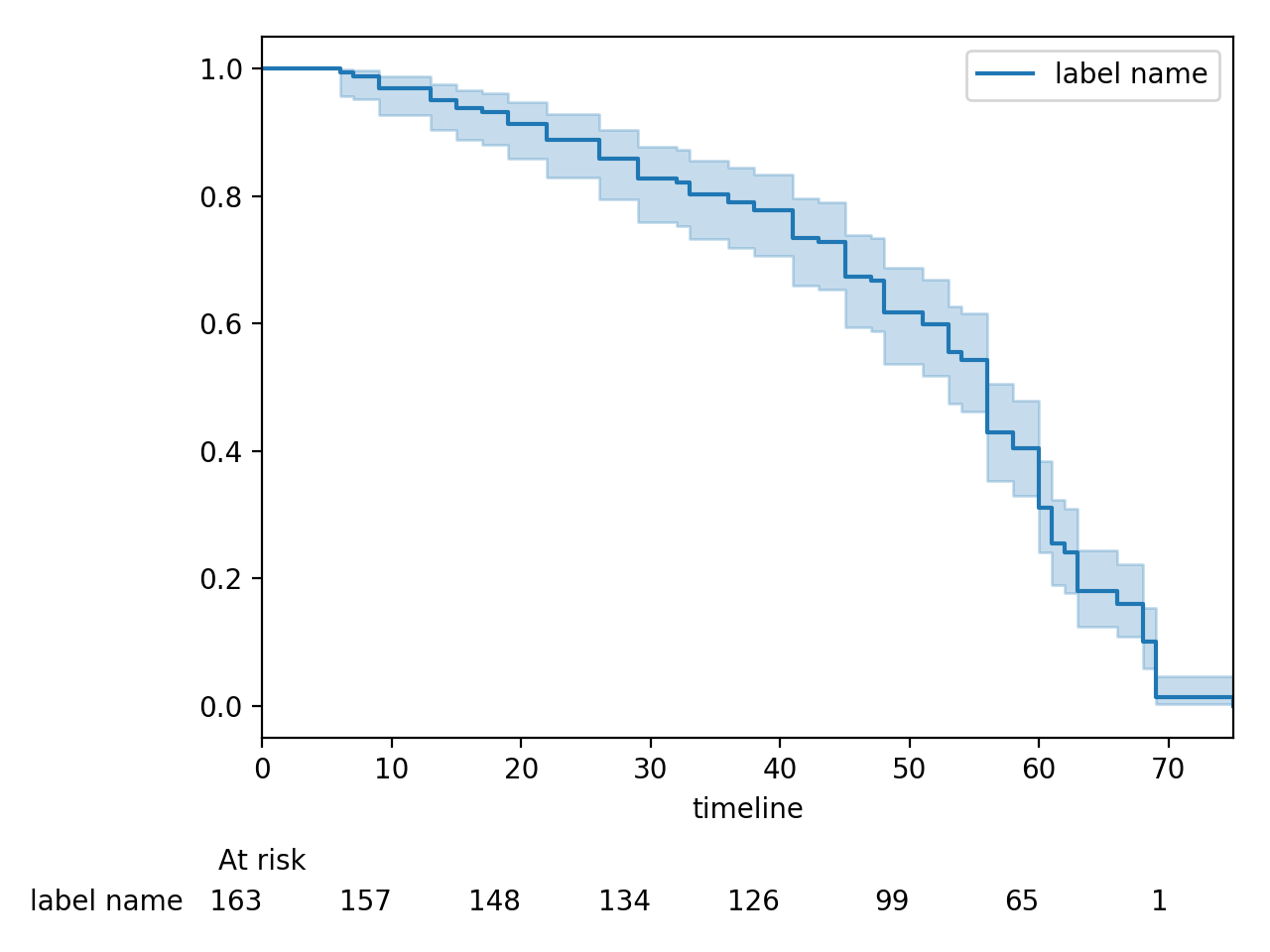
Displaying at-risk counts below plots¶
kmf.fit(T, E, label="label name")
kmf.plot_survival_function(at_risk_counts=True)
plt.tight_layout()
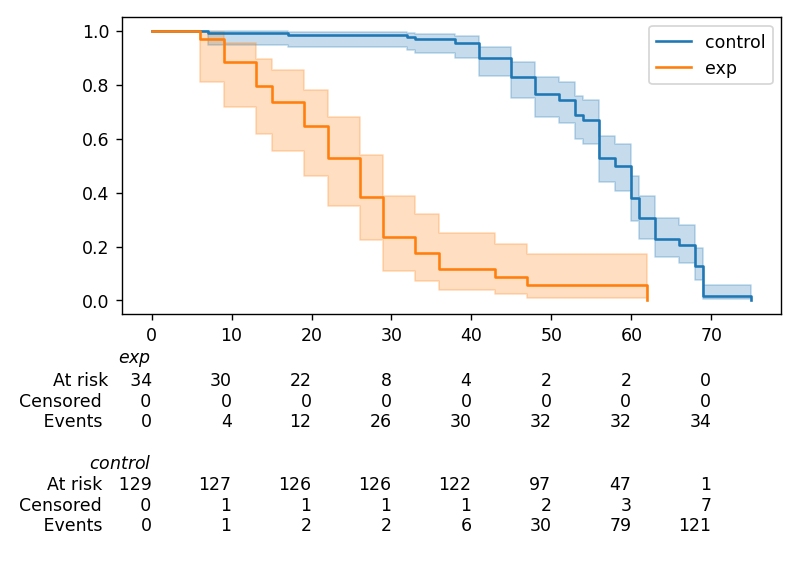
Displaying multiple at-risk counts below plots¶
The function lifelines.plotting.add_at_risk_counts() allows you to add counts at the bottom of your figures. For example:
from lifelines import KaplanMeierFitter
from lifelines.datasets import load_waltons
waltons = load_waltons()
ix = waltons['group'] == 'control'
ax = plt.subplot(111)
kmf_control = KaplanMeierFitter()
ax = kmf_control.fit(waltons.loc[ix]['T'], waltons.loc[ix]['E'], label='control').plot_survival_function(ax=ax)
kmf_exp = KaplanMeierFitter()
ax = kmf_exp.fit(waltons.loc[~ix]['T'], waltons.loc[~ix]['E'], label='exp').plot_survival_function(ax=ax)
from lifelines.plotting import add_at_risk_counts
add_at_risk_counts(kmf_exp, kmf_control, ax=ax)
plt.tight_layout()
will display
Transforming survival-table data into lifelines format¶
Some lifelines classes are designed for lists or arrays that represent one individual per row. If you instead have data in a survival table format, there exists a utility method to get it into lifelines format.
Example: Suppose you have a CSV file with data that looks like this:
time |
observed deaths |
censored |
|---|---|---|
0 |
7 |
0 |
1 |
1 |
1 |
2 |
2 |
0 |
3 |
1 |
2 |
4 |
5 |
2 |
… |
… |
… |
import pandas as pd
from lifelines.utils import survival_events_from_table
df = pd.read_csv('file.csv')
df = df.set_index('time')
T, E, W = survival_events_from_table(df, observed_deaths_col='observed deaths', censored_col='censored')
# weights, W, is the number of occurrences of each observation - helps with data compression.
kmf = KaplanMeierFitter().fit(T, E, weights=W)
Transforming observational data into survival-table format¶
Perhaps you are interested in viewing the survival table given some durations and censoring vectors.
from lifelines.utils import survival_table_from_events
table = survival_table_from_events(T, E)
print(table.head())
"""
removed observed censored entrance at_risk
event_at
0 0 0 0 60 60
2 2 1 1 0 60
3 3 1 2 0 58
4 5 3 2 0 55
5 12 6 6 0 50
"""
Set the index/timeline of a estimate¶
Suppose your dataset has lifetimes grouped near time 60, thus after fitting
lifelines.fitters.kaplan_meier_fitter.KaplanMeierFitter, you survival function might look something like:
print(kmf.survival_function_)
"""
KM-estimate
0 1.00
47 0.99
49 0.97
50 0.96
51 0.95
52 0.91
53 0.86
54 0.84
55 0.79
56 0.74
57 0.71
58 0.67
59 0.58
60 0.49
61 0.41
62 0.31
63 0.24
64 0.19
65 0.14
66 0.10
68 0.07
69 0.04
70 0.02
71 0.01
74 0.00
"""
What you would like is to have a predictable and full index from 40 to 75. (Notice that
in the above index, the last two time points are not adjacent – the cause is observing no lifetimes
existing for times 72 or 73). This is especially useful for comparing multiple survival functions at specific time points. To do this, all fitter methods accept a timeline argument:
kmf.fit(T, timeline=range(40,75))
print(kmf.survival_function_)
"""
KM-estimate
40 1.00
41 1.00
42 1.00
43 1.00
44 1.00
45 1.00
46 1.00
47 0.99
48 0.99
49 0.97
50 0.96
51 0.95
52 0.91
53 0.86
54 0.84
55 0.79
56 0.74
57 0.71
58 0.67
59 0.58
60 0.49
61 0.41
62 0.31
63 0.24
64 0.19
65 0.14
66 0.10
67 0.10
68 0.07
69 0.04
70 0.02
71 0.01
72 0.01
73 0.01
74 0.00
"""
lifelines will intelligently forward-fill the estimates to unseen time points.
Example SQL query to get survival data from a table¶
Below is a way to get an example dataset from a relational database (this may vary depending on your database):
SELECT
id,
DATEDIFF('dd', started_at, COALESCE(ended_at, CURRENT_DATE)) AS "T",
(ended_at IS NOT NULL) AS "E"
FROM table
Explanation¶
Each row is an id, a duration, and a boolean indicating whether the event occurred or not. Recall that we denote a
“True” if the event did occur, that is, ended_at is filled in (we observed the ended_at). Ex:
id |
T |
E |
|---|---|---|
10 |
40 |
True |
11 |
42 |
False |
12 |
42 |
False |
13 |
36 |
True |
14 |
33 |
True |
Example SQL queries and transformations to get time varying data¶
For Cox time-varying models, we discussed what the dataset should look like in Dataset creation for time-varying regression. Typically we have a base dataset, and then we fold in the covariate datasets. Below are some SQL queries and Python transformations from end-to-end.
Base dataset: base_df¶
SELECT
id,
group,
DATEDIFF('dd', dt.started_at, COALESCE(dt.ended_at, CURRENT_DATE)) AS "T",
(ended_at IS NOT NULL) AS "E"
FROM dimension_table dt
Time-varying variables: cv¶
-- this could produce more than 1 row per subject
SELECT
id,
DATEDIFF('dd', dt.started_at, ft.event_at) AS "time",
ft.var1
FROM fact_table ft
JOIN dimension_table dt
USING(id)
from lifelines.utils import to_long_format
from lifelines.utils import add_covariate_to_timeline
base_df = to_long_format(base_df, duration_col="T")
df = add_covariate_to_timeline(base_df, cv, duration_col="time", id_col="id", event_col="E")
Event variables: event_df¶
Another very common operation is to add event data to our time-varying dataset. For example, a dataset/SQL table that contains information about the dates of an event (and NULLS if the event didn’t occur). An example SQL query may look like:
SELECT
id,
DATEDIFF('dd', dt.started_at, ft.event1_at) AS "E1",
DATEDIFF('dd', dt.started_at, ft.event2_at) AS "E2",
DATEDIFF('dd', dt.started_at, ft.event3_at) AS "E3"
...
FROM dimension_table dt
In Pandas, this may look like:
"""
id E1 E2 E3
0 1 1.0 NaN 2.0
1 2 NaN 5.0 NaN
2 3 3.0 5.0 7.0
...
"""
Initially, this can’t be added to our baseline time-varying dataset. Using lifelines.utils.covariates_from_event_matrix() we can convert a DataFrame like this into one that can be easily added.
from lifelines.utils import covariates_from_event_matrix
cv = covariates_from_event_matrix(event_df, id_col='id')
print(cv)
"""
id duration E1 E2 E3
0 1 1.0 1 0 0
1 1 2.0 0 1 0
2 2 5.0 0 1 0
3 3 3.0 1 0 0
4 3 5.0 0 1 0
5 3 7.0 0 0 1
"""
base_df = add_covariate_to_timeline(base_df, cv, duration_col="time", id_col="id", event_col="E")
Example cumulative sums over time-varying covariates¶
Often we have either transactional covariate datasets or state covariate datasets. In a transactional dataset, it may make sense to sum up the covariates to represent administration of a treatment over time. For example, in the risky world of start-ups, we may want to sum up the funding amount received at a certain time. We also may be interested in the amount of the last round of funding. Below is an example to do just that:
Suppose we have an initial DataFrame of start-ups like:
seed_df = pd.DataFrame([
{'id': 'FB', 'E': True, 'T': 12, 'funding': 0},
{'id': 'SU', 'E': True, 'T': 10, 'funding': 0},
])
And a covariate DataFrame representing funding rounds like:
cv = pd.DataFrame([
{'id': 'FB', 'funding': 30, 't': 5},
{'id': 'FB', 'funding': 15, 't': 10},
{'id': 'FB', 'funding': 50, 't': 15},
{'id': 'SU', 'funding': 10, 't': 6},
{'id': 'SU', 'funding': 9, 't': 10},
])
We can do the following to get both the cumulative funding received and the latest round of funding:
from lifelines.utils import to_long_format
from lifelines.utils import add_covariate_to_timeline
df = seed_df.pipe(to_long_format, 'T')\
.pipe(add_covariate_to_timeline, cv, 'id', 't', 'E', cumulative_sum=True)\
.pipe(add_covariate_to_timeline, cv, 'id', 't', 'E', cumulative_sum=False)
"""
start cumsum_funding funding stop id E
0 0 0.0 0.0 5.0 FB False
1 5 30.0 30.0 10.0 FB False
2 10 45.0 15.0 12.0 FB True
3 0 0.0 0.0 6.0 SU False
4 6 10.0 10.0 10.0 SU False
5 10 19.0 9.0 10.0 SU True
"""
Sample size determination under a CoxPH model¶
Suppose you wish to measure the hazard ratio between two populations under the CoxPH model. That is, we want to evaluate the hypothesis
H0: relative hazard ratio = 1 vs H1: relative hazard ratio != 1, where the relative hazard ratio is \(\exp{\left(\beta\right)}\) for the experiment group vs the control group. A priori, we are interested in the sample sizes of the two groups necessary to achieve a certain statistical power. To do this in lifelines, there is the lifelines.statistics.sample_size_necessary_under_cph() function. For example:
from lifelines.statistics import sample_size_necessary_under_cph
desired_power = 0.8
ratio_of_participants = 1.
p_exp = 0.25
p_con = 0.35
postulated_hazard_ratio = 0.7
n_exp, n_con = sample_size_necessary_under_cph(desired_power, ratio_of_participants, p_exp, p_con, postulated_hazard_ratio)
# (421, 421)
This assumes you have estimates of the probability of event occurring for both the experiment and control group. This could be determined from previous experiments.
Power determination under a CoxPH model¶
Suppose you wish to measure the hazard ratio between two populations under the CoxPH model. To determine the statistical power of a hazard ratio hypothesis test, under the CoxPH model, we can use lifelines.statistics.power_under_cph(). That is, suppose we want to know the probability that we reject the null hypothesis that the relative hazard ratio is 1, assuming the relative hazard ratio is truly different from 1. This function will give you that probability.
from lifelines.statistics import power_under_cph
n_exp = 50
n_con = 100
p_exp = 0.25
p_con = 0.35
postulated_hazard_ratio = 0.5
power = power_under_cph(n_exp, n_con, p_exp, p_con, postulated_hazard_ratio)
# 0.4957
Problems with convergence in the Cox proportional hazard model¶
Since the estimation of the coefficients in the Cox proportional hazard model is done using the Newton-Raphson algorithm, there are sometimes problems with convergence. Here are some common symptoms and resolutions:
First check: look for
ConvergenceWarningin the output. Most often problems in convergence are the result of problems in the dataset. lifelines has checks it runs against the dataset before fitting and warnings are outputted to the user.delta contains nan value(s).: First try addingshow_progress=Truein thefitfunction. If the values indeltagrow unbounded, it’s possible thestep_sizeis too large. Try setting it to a small value (0.1-0.5).Convergence halted due to matrix inversion problems: This means that there is high collinearity in your dataset. That is, a column is equal to the linear combination of 1 or more other columns. A common cause of this error is dummying categorical variables but not dropping a column, or some hierarchical structure in your dataset. Try to find the relationship by:adding a penalizer to the model, ex: CoxPHFitter(penalizer=0.1).fit(…) until the model converges. In the print_summary(), the coefficients that have high collinearity will have large (absolute) magnitude in the coefs column.
using the variance inflation factor (VIF) to find redundant variables.
looking at the correlation matrix of your dataset, or
Some coefficients are many orders of magnitude larger than others, and the standard error of the coefficient is also large or there are
nan’s in the results. This can be seen using theprint_summarymethod on a fittedCoxPHFitterobject.Look for a
ConvergenceWarningabout variances being too small. The dataset may contain a constant column, which provides no information for the regression (Cox model doesn’t have a traditional “intercept” term like other regression models).The data is completely separable, which means that there exists a covariate the completely determines whether an event occurred or not. For example, for all “death” events in the dataset, there exists a covariate that is constant amongst all of them. Look for a
ConvergenceWarningafter thefitcall. See https://stats.stackexchange.com/questions/11109/how-to-deal-with-perfect-separation-in-logistic-regressionRelated to above, the relationship between a covariate and the duration may be completely determined. For example, if the rank correlation between a covariate and the duration is very close to 1 or -1, then the log-likelihood can be increased arbitrarily using just that covariate. Look for a
ConvergenceWarningafter thefitcall.Another problem may be a collinear relationship in your dataset. See point 3. above.
If adding a very small
penalizersignificantly changes the results (CoxPHFitter(penalizer=0.0001)), then this probably means that the step size in the iterative algorithm is too large. Try decreasing it (.fit(..., step_size=0.50)or smaller), and returning thepenalizerterm to 0.If using the
strataargument, make sure your stratification group sizes are not too small. Trydf.groupby(strata).size().
Adding weights to observations in a Cox model¶
There are two common uses for weights in a model. The first is as a data size reduction technique (known as case weights). If the dataset has more than one subjects with identical attributes, including duration and event, then their likelihood contribution is the same as well. Thus, instead of computing the log-likelihood for each individual, we can compute it once and multiple it by the count of users with identical attributes. In practice, this involves first grouping subjects by covariates and counting. For example, using the Rossi dataset, we will use Pandas to group by the attributes (but other data processing tools, like Spark, could do this as well):
from lifelines.datasets import load_rossi
rossi = load_rossi()
rossi_weights = rossi.copy()
rossi_weights['weights'] = 1.
rossi_weights = rossi_weights.groupby(rossi.columns.tolist())['weights'].sum()\
.reset_index()
The original dataset has 432 rows, while the grouped dataset has 387 rows plus an additional weights column. CoxPHFitter has an additional parameter to specify which column is the weight column.
from lifelines import CoxPHFitter
cph = CoxPHFitter()
cph.fit(rossi_weights, 'week', 'arrest', weights_col='weights')
The fitting should be faster, and the results identical to the unweighted dataset. This option is also available in the CoxTimeVaryingFitter.
The second use of weights is sampling weights. These are typically positive, non-integer weights that represent some artificial under/over sampling of observations (ex: inverse probability of treatment weights). It is recommended to set robust=True in the call to the fit as the usual standard error is incorrect for sampling weights. The robust flag will use the sandwich estimator for the standard error.
Warning
The implementation of the sandwich estimator does not handle ties correctly (under the Efron handling of ties), and will give slightly or significantly different results from other software depending on the frequency of ties.
Correlations between subjects in a Cox model¶
There are cases when your dataset contains correlated subjects, which breaks the independent-and-identically-distributed assumption. What are some cases when this may happen?
If a subject appears more than once in the dataset (common when subjects can have the event more than once)
If using a matching technique, like propensity-score matching, there is a correlation between pairs.
In both cases, the reported standard errors from a unadjusted Cox model will be wrong. In order to adjust for these correlations, there is a cluster_col keyword in fit() that allows you to specify the column in the DataFrame that contains designations for correlated subjects. For example, if subjects in rows 1 & 2 are correlated, but no other subjects are correlated, then cluster_col column should have the same value for rows 1 & 2, and all others unique. Another example: for matched pairs, each subject in the pair should have the same value.
from lifelines.datasets import load_rossi
from lifelines import CoxPHFitter
rossi = load_rossi()
# this may come from a database, or other libraries that specialize in matching
matched_pairs = [
(156, 230),
(275, 228),
(61, 252),
(364, 201),
(54, 340),
(130, 33),
(183, 145),
(268, 140),
(332, 259),
(314, 413),
(330, 211),
(372, 255),
# ...
]
rossi['id'] = None # we will populate this column
for i, pair in enumerate(matched_pairs):
subjectA, subjectB = pair
rossi.loc[subjectA, 'id'] = i
rossi.loc[subjectB, 'id'] = i
rossi = rossi.dropna(subset=['id'])
cph = CoxPHFitter()
cph.fit(rossi, 'week', 'arrest', cluster_col='id')
Specifying cluster_col will handle correlations, and invoke the robust sandwich estimator for standard errors (the same as setting robust=True).
Serialize a lifelines model to disk¶
When you want to save (and later load) a lifelines model to disk, you can use the loads and dumps API from most popular serialization library (dill, pickle, joblib):
from dill import loads, dumps
from pickle import loads, dumps
s_cph = dumps(cph)
cph_new = loads(s_cph)
cph_new.summary
s_kmf = dumps(kmf)
kmf_new = loads(s_kmf)
kmf_new.survival_function_
The codes above save the trained models as binary objects in memory. To serialize a lifelines model to a given path on disk:
import pickle
with open('/path/my.pickle', 'wb') as f:
pickle.dump(cph, f) # saving my trained cph model as my.pickle
with open('/path/my.pickle', 'rb') as f:
cph_new = pickle.load(f)
cph_new.summary # should produce the same output as cph.summary
Produce a LaTex or HTML table¶
New in version 0.23.1, lifelines models now have the ability to output a LaTeX or HTML table from the print_summary option:
from lifelines.datasets import load_rossi
from lifelines import CoxPHFitter
rossi = load_rossi()
cph = CoxPHFitter().fit(rossi, 'week', 'arrest')
# print a LaTeX table:
cph.print_summary(style="latex")
# print a HTML summary and table:
cph.print_summary(style="html")
In order to use the produced table summary in LaTeX, make sure you import the package booktabs in your preamble (\usepackage{booktabs}), since it is required to display the table properly.
Filter a print_summary table¶
The information provided by print_summary can be a lot, and even too much for some screens. You can filter to specific columns use the columns kwarg (default is to display all columns):
from lifelines.datasets import load_rossi
from lifelines import CoxPHFitter
rossi = load_rossi()
cph = CoxPHFitter().fit(rossi, 'week', 'arrest')
cph.print_summary(columns=["coef", "se(coef)", "p"])
Fixing a FormulaSyntaxError¶
As a of lifelines v0.25.0, formulas can be used to model your dataframe. This may cause problems if your dataframe has column names with spaces, periods, or other characters. The cheapest way to fix this is to change your column names:
df = pd.DataFrame({
'T': [1, 2, 3, 4],
'column with spaces': [1.5, 1.0, 2.5, 1.0],
'column.with.periods': [2.5, -1.0, -2.5, 1.0],
'column': [2.0, 1.0, 3.0, 4.0]
})
cph = CoxPHFitter().fit(df, 'T')
"""
FormulaSyntaxError:
...
"""
df.columns = df.columns.str.replace(' ', '')
df.columns = df.columns.str.replace('.', '')
cph = CoxPHFitter().fit(df, 'T')
"""
👍
"""
Another option is to use the formula syntax to handle this:
df = pd.DataFrame({
'T': [1, 2, 3, 4],
'column with spaces': [1.5, 1.0, 2.5, 1.0],
'column.with.periods': [2.5, -1.0, -2.5, 1.0],
'column': [2.0, 1.0, 3.0, 4.0]
})
cph = CoxPHFitter().fit(df, 'T', formula="column + Q('column with spaces') + Q('column.with.periods')")